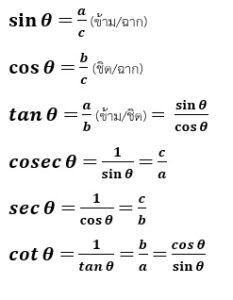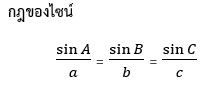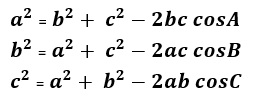สรุป ตรีโกณมิติ คืออะไร และทุกเรื่องที่ควรรู้ของ ตรีโกณมิติ

ตรีโกณมิติ คืออะไร

ตรีโกณมิติ (Trigonometry) คือ สาขาของคณิตศาสตร์ที่เกี่ยวข้องกับมุม, รูปสามเหลี่ยม และฟังก์ชันตรีโกณมิติ เช่น ไซน์ และ โคไซน์ มีความเกี่ยวข้องกับเรขาคณิต แม้ว่าจะสรุปไม่ได้อย่างแน่ชัดว่า ตรีโกณมิติเป็นหัวข้อย่อยของเรขาคณิต

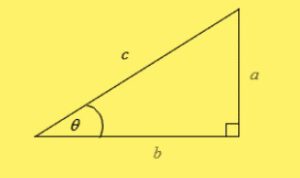
จากรูป สามเหลี่ยมมุมฉาก

จะได้ว่า

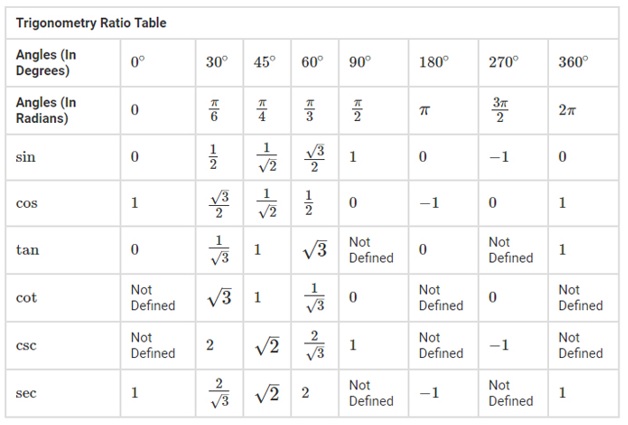
ค่า sin⁡θ cos⁡θ tan⁡θ ของมุมพื้นฐานมีค่าเท่าไหร่บ้าง

ฟังก์ชันไซน์และโคไซน์

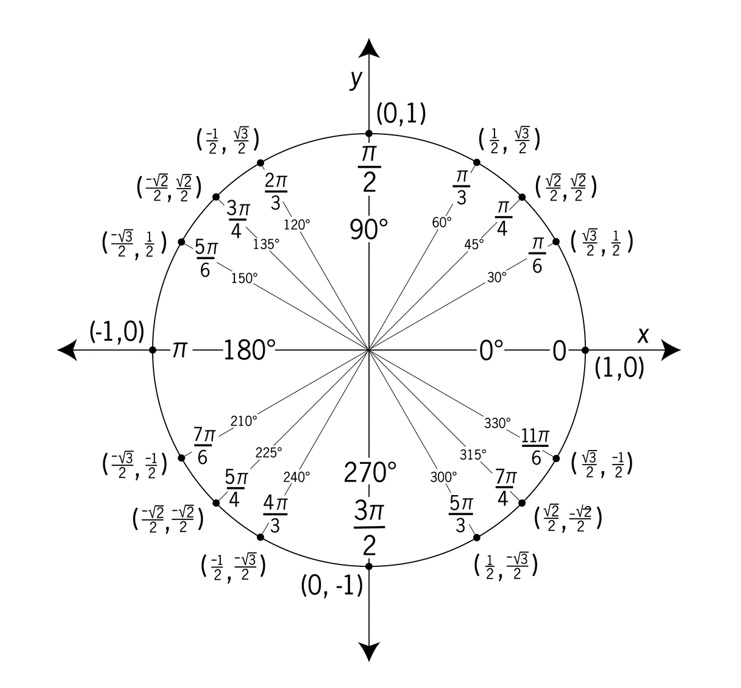
การกำหนดค่าของฟังก์ชันตรีโกณมิตินั้น สามารถทำได้โดยการใช้วงกลมรัศมี 1 หน่วย มีจุดศูนย์กลางอยู่ที่จุดกำเนิดและเราจะเรียกวงกลมดังกล่าวว่า วงกลมหนึ่งหน่วย (The unit circle)

เมื่อเรากำหนดจำนวนจริง θ (ทีตา) จาก (1,0) วัดระยะไปตามส่วนโค้งของวงกลม โดยมีข้อตกลงดังนี้ว่า :

ถ้า θ > 0 จะวัดส่วนโค้งจากจุด (1,0) ไปในทิศทางทวนเข็มนาฬิกา

ถ้า θ < 0 จะวัดส่วนโค้งจากจุด (1,0) ไปในทิศทางตามเข็มนาฬิกา

ถ้า θ = 0 จุดปลายส่วนโค้งคือจุด (1,0)

จะได้ว่า เมื่อเรากำหนดจำนวนจริง θ ให้ เราสามรารถหาจุด (x,y) ซึ่งเป็นจุดปลายส่วนโค้งได้เพียงจุดเดียวเท่านั้น

ถ้า |θ| > 2π แสดงว่า วัดส่วนโค้งเกิน 1 รอบ เพราะเส้นรองวงของวงกลมยาว 2π หน่วย

เมื่อ (x,y) เป็นจุดปลายส่วนโค้งของวงกลมข้างต้น

y = sinθ

x = cosθ

ฟังก์ชันไซน์และฟังก์ชันโคไซน์นั้น เป็นจำนวนจริง ตั้งแต่ –1 ถึง 1

นั่นคือ เรนจ์ของฟังก์ชันไซน์และโคไซน์ คือ เซตของจำนวนจริง ตั้งแต่ –1 ถึง 1

และโดเมนของฟังก์ชันทั้งสองคือเซตของจำนวนจริง

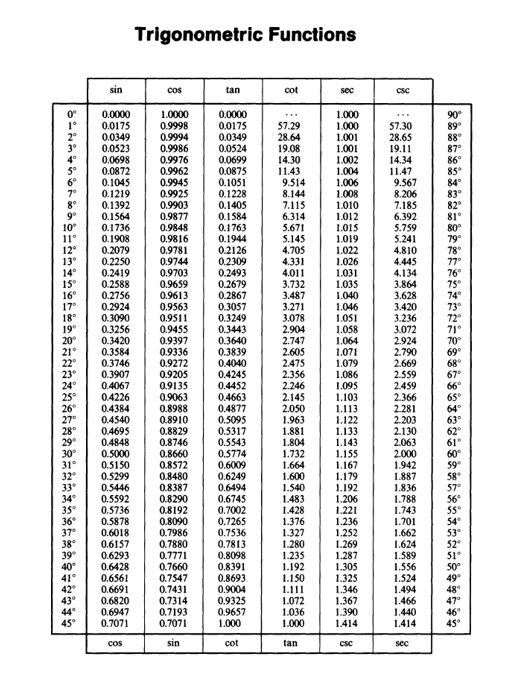
ตารางค่าฟังก์ชันตรีโกณมิติ

หาค่ามุมที่ต้องการทางด้านซ้ายมือของตาราง แล้วนำมาเทียบกับค่าฟังก์ชันตรีโกณมิติทางด้านขวามือของตาราง

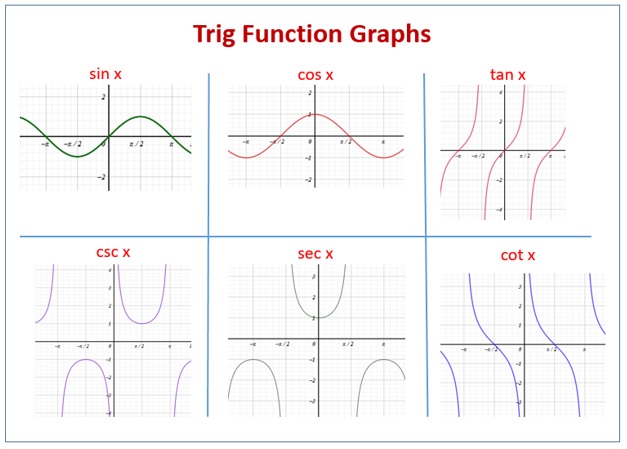
กราฟของฟังก์ชันตรีโกณมิติ

จากรูปข้างต้น จะเห็นได้ว่า

คาบของกราฟ y = sinx และ y = cosx เท่ากับ 2π

คาบของกราฟ y = cosecx และ y = secx เท่ากับ 2π

คาบของกราฟ y = tanx และ y = cotx เท่ากับ π

สำหรับฟังก์ชันที่เป็นคาบซึ่งมีค่าสูงสุดและค่าต่ำสุด เราจะเรียกว่าที่เท่ากับครึ่งหนึ่งของค่าสูงสุดลบด้วยค่าต่ำสุดของฟังก์ชันนี้ว่า แอมพลิจูด (Amplitude) โดยฟังก์ชัน y = sinx และ y = cosx มีแอมพลิจูดเป็น 1 เท่ากัน

ตัวผกผันของฟังก์ชันตรีโกณมิติ

ฟังก์ชันตรีโกณมิติทั้งหกฟังก์ชันสามารถหาอินเวอร์สได้โดยสลับที่ระหว่างโดเมนและเรนจ์ตามปรกติ (กลายเป็น x = siny) แต่อินเวอร์สที่ได้เหล่านี้จะไม่เป็นฟังก์ชัน เพราะค่า x แต่ละค่านั้น ให้ค่า y ได้หลายค่าไม่มีที่สิ้นสุด ดังนั้น หากจะกำหนดอินเวิร์สของฟังก์ชันตรีโกณมิติให้เป็นฟังก์ชันด้วย ก็จำเป็นต้องจำกัดข่วงของเรนจ์ด้วย นั่นหมายถึง ความหมายของ x = siny และความหมายของ y = arcsinx ไม่เท่ากัน เนื่องจากเรนจ์ไม่เท่ากัน เราเรียกฟังก์ชันผกผันของตรีโกณมิติโดยใช้คำว่า arc นำหน้า เช่น arcsin arccos arctan เป็นต้น

เอกลักษณ์และสมการตรีโกณมิติ

เอกลักษณ์ตรีโกณมิติ คือ การเท่ากันของฟังก์ชันตรีโกณมิติที่ต่างกัน และเป็นจริงสำหรับทุก ๆ ค่าของขนาดของมุม

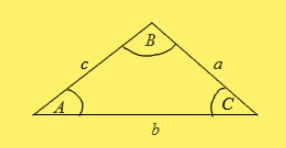
กฎของโคไซน์และไซน์

ให้ ABC เป็นสามเหลี่ยมใด ๆ

กฎของไซน์

กฎของโคไซน์

ตัวอย่างข้อสอบเรื่อง ตรีโกณมิติ

Related Posts

เซต

ตรรกศาสตร์

การให้เหตุผล

จำนวนจริง

ทฤษฎีจำนวนเบื้องต้น

คณิต สรุป เมทริกซ์ คืออะไร พร้อมตัวอย่างข้อสอบ