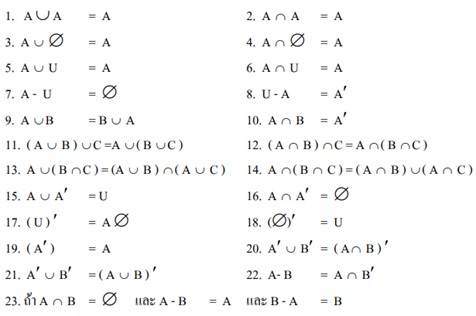เซต คืออะไร
เซต คือ กลุ่มของสมาชิก (element) ของสิ่งที่สนใจ เช่น เซตของวันในหนึ่งสัปดาห์ หมายถึง กลุ่มของวันจันทร์ อังคาร พุธ พฤหัสบดี ศุกร์ เสาร์ และอาทิตย์ เป็นต้น ซึ่งคำว่าเซตนั้นมีคุณสมบัติที่สำคัญคือ ต้องสามารถระบุได้ว่า อะไรอยู่ในเซต อะไรไม่อยู่ในเซต โดยเราสามารถเขียนเซตได้ 3 รูปแบบ ดังนี้
1.การเขียนเป็นข้อความ (Statement Form) เป็นการเขียนข้อความเพื่อแสดงความชัดเจน เช่น เซตของนักศึกษาที่ลงทะเบียนเรียนวิชา มธ.151 เซตของจำนวนเฉพาะที่ไม่เกิน 50 เซตของจำนวนเต็มบวกที่คูณกับ 5 แล้วได้ไม่เกิน 8 เป็นต้น
2.การเขียนแจกแจงสมาชิก (Tabular Form / Roaster Method) เป็นการเขียนแจกแจงสมาชิกทุกตัวลงในเครื่องหมายวงเล็บปีกกาที่มีลักษณะ { } และใช้เครื่องหมายจุลภาค ( , ) คั่นสมาชิกแต่ละตัว เช่น เซตของจำนวนนับที่น้อยกว่า 5 เขียนแทนด้วย {1, 2. 3, 4} โดยทั่วไปจะแทนเซตด้วยอักษรภาษาอังกฤษตัวพิมพ์ใหญ่ เช่น A, B, C และแทนสมาชิกด้วยตัวพิมพ์เล็ก เช่น a, b, c
หมายเหตุ : เราจะใช้จุดสามจุด (…) เพื่อแสดงว่ามีสมาชิกอื่น ๆ อีก ซึ่งเป็นที่เข้าใจตรงกันอยู่แล้วว่ามีอะไรในเซทบ้าง เช่น {1, 2, … , 10} หมายถึง เข้าใจว่ามี 3, 4, 5, 6, 7, 8, 9 เป็นสมาชิกของเซตด้วย หรือใช้แทนเซตอนันต์ที่บอกว่ามีจำนวนอีกมากมายไม่สิ้นสุด
3. การแจกแจงเงื่อนไช (Set Builder Form/ Rule Method) เป็นการใช้ตัวแปรเขียนแทนสมาชิกแล้วทำการบรรยายสมบัติของสมาชิกที่อยู่ในรูปตัวแปร เช่น A = {x | x เป็นพยัญชนะสามตัวแรกในภาษาอังกฤษ} อ่านว่า A เป็นเซตซึ่งประกอบไปด้วยสมาชิก x โดยที่ x เป็นพยัญชนะสามตัวแรกในภาษาอังกฤษ เครื่องหมาย “|”แทนคำว่า “โดยที่” เราสามารถเขียนรูปแบบการแจกแจงเงื่อนไขให้อยู่ในรูปแจกแจงสมาชิกได้ทุกเซต แต่ในบางเซต เราไม่สามารถเขียนรูปแบบการแจกแจงสมาชิกให้อยู่ในรูปเงื่อนไขได้
ชนิดของเซท
- เซตว่าง (Empty Set หรือ Null Set) หมายถึง เซทที่ไม่มีสมาชิกหรืออาจะกล่าวได้ว่าเซตว่างมีสมาชิก 0 สมาชิก โยสัญลักษณ์ที่ใช้ คือ { }
- เซตจำกัด (Finite Set) หมายถึง เซตที่สามารถนับจำนวนสมาชิกได้ครบถ้วน สามารถบอกได้ว่ามีจำนวนสมาชิกเท่าใด เป็นจำนวนเต็มบวกหรือศูนย์
- เซตอนันต์ (Infinite Set) หมายถึง เซตที่มีจำนวนสมาชิกมากมายนับไม่ถ้วน ไม่สามารถบอกได้ว่ามีจำนวนเท่าใด
- เซตเท่ากัน (Equal Set) หมายถึง เมื่อ A และ B เป็นเซตใดๆ A จะเรียกว่าเท่ากับ B ก็ต่อเมื่อเซตทั้งสองมีจำนวนสมาชิกเท่ากันและเหมือนกันทุกสมาชิก ซึ่งจะเขียนแทนด้วยสัญลักษณ์ A – B หรืออาจกล่าวได้ว่าเซตสองเซตใดๆ จะเท่ากันก็ต่อเมื่อสมาชิกของ A ทุกสมาชิกเป็นสมาชิกของ B และสมาชิกทุกสมาชิกของ B เป็นสมาชิกของ A นั่นคือ A = B ก็ต่อเมื่อ ถ้า x ϵ A แล้ว X ϵ B และ ถ้า X ϵ B แล้ว X ϵ A
- เซตเสมอเหมือนกัน (Equivalent Set) คือ เซต 2 เซตใดๆ ที่มีจำนวนสมาชิกเท่ากันแต่ไม่เหมือนกันทุกตัว เรียกว่า เซตเสมอ ฃเหมือน A เสมอเหมือน B จะเขียนแทนด้วย A ≡ B นั่นคือเซต 2 เซตที่เท่ากันเสมอเหมือนกัน แต่เซต 2 เซตที่เสมอเหมือนกันอาจจะเท่ากัน หรือไม่เท่ากันก็ได้
- สับเซต (Sub Set) กำหนด A และ B เป็นเซตใดๆ A จะเรียกเป็นสับเซตของ B ซึ่งเขียนแทนด้วยสัญลักษณ์ A C Bก็ต่อเมื่อ X ϵ A แล้ว X ϵ B
- พาวเวอร์เซท (Power Set) คือ เซตของสับเซตทั้งหมดของเซต A เมื่อ A เป็นเซตจำกัด เพาเวอร์เซตของเซต A เขียนแทนด้วย P(A)
เอกภพสัมพัทธ์และแผนภาพเวนน์-ออยเลอร์
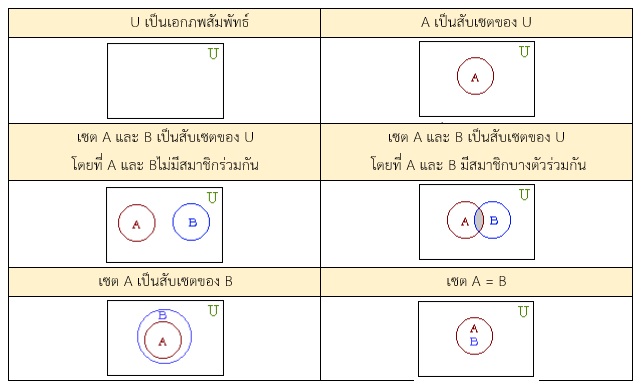
เอกภพสัมพัทธ์ (Relatively Universe) คือ เซตที่กำหนดขึ้น โดยมีข้อตกลงว่า ต่อไปจะกล่าวถึงสมาชิกของเซตนี้เท่านั้น จะไม่มีการกล่าวถึงสิ่งใดที่ไม่เป็นสมาชิกของเซตนี้ นิยมใช้สัญลักษณ์ U แทนสัญลักษณ์เอกภพสัมพัทธ์
แผนภาพของเวนน์-ออยเลอร์ (Venn-Euler) คือ แผนภาพที่ใช้เพื่อให้การศึกษาเกี่ยวกับเซตให้เข้าใจง่ายมากยิ่งขึ้น โดยจะแทนเอกภพสัมพัทธ์ด้วยสี่เหลี่ยมมุมฉาก และแทนเซตอื่น ๆ ด้วยวงกลมหรือรูปเรขาคณิตอื่นๆ สมาชิกของเอกกพสัมพันธ์อยู่ภายในรูปสี่เหลี่ยม และสมาชิกของ A อยู่ภายในวงกลม
การดำเนินการระหว่างเซต
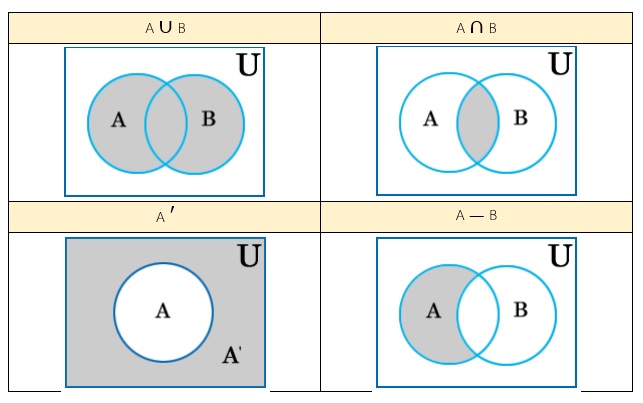
- ยูเนียน (Union) : ยูเนียนของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต A หรือ B เขียนแทนด้วย A ∪ B
- อินเตอร์เซคชัน (Intersection) : อินเตอร์เซคชันของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกของเซต A และ B เขียนแทนด้วย A ∩ B
- คอมพลีเมนต์ (Complement) : คอมพลีเมนต์ของเซต A คือเซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของเอกภพสัมพัทธ์ แต่ไม่เป็นสมาชิกของ A เขียนแทนด้วย A ‘
- ผลต่างของเซต (Difference) : ผลต่างของเซต A และ B คือเซตที่ประกอบด้วยสมาชิกที่เปีนสมาชิกของเซต A แต่ไม่เป็นสมาชิกของเซต B เขียนแทนด้วย A — B
สมบัติของเซตที่ควรรู้
ตัวอย่างข้อสอบเรื่อง เซต
1. กำหนด A = {x | x เป็นพยัญชนะในคำว่า “สุดสวย”},
B = {x | x เป็นพยัญชนะในคำว่า “สวยสด”},
C = {x | x เป็นพยัญชนะในคำว่า “สายวาด”},
D = {x | x เป็นพยัญชนะในคำว่า “สายสวย”}
ข้อใดต่อไปนี้เป็นจริง
ก. A = D
ข. C = D
ค. B = D
ง. A = B
2. เซตในข้อใดเป็นเซตจำกัด
ก. {x | x เป็นจำนวนเต็มคู่}
ข. {x | x เป็นจำนวนเต็มคู่ที่น้อยกว่า 10}
ค. {x | x เป็นจำนวนเต็มมากกว่า 1}
ง. {x | x เป็นจำนวนเต็ม และ 3 < x < 10}
3. กำหนดให้ A = {a} ดังนั้นจานวนสมาชิกของ P(P(P(A)))) เท่ากับข้อใดต่อไปนี้
ก. 4
ข. 8
ค. 16
ง. 32
4. กำหนดให้ A = {1, 2, 3}, B = {6, 7, 8} จงหา A ∩ B
ก. { }
ข. {1, 2, 3}
ค. {6, 7, 8}
ง. {1, 2, 3, 6, 7, 8}
5.เซตใดต่อไปนี้ ไม่เป็น เซตว่าง
ก. {x | x ∈ R และ x2 = -1}
ข. {x | x ∈ I และ x + 1 = x}
ค. {x | x ∈ R และ x + x = 0}
ง. {x | x ∈ I และ x2 < 0}