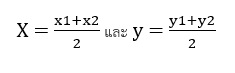คณิต สรุป เรขาคณิตวิเคราะห์และภาคตัดกรวย

สรุปเนื้อหาเรื่อง เรขาคณิตวิเคราะห์และภาคตัดกรวย

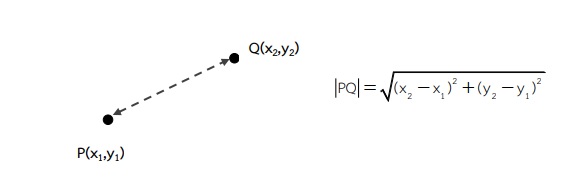
ระยะทางระหว่างจุดสองจุด

จากรูป สัญลักษณ์ที่ใช้แทนระยะทางระหว่างจุด P กับ Q คือ |PQ| หรือ PQ

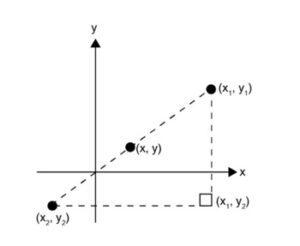
จุดกึ่งกลางระหว่างจุดสองจุด

จากรูป

ถ้าจุด (x, y) เป็นจุดกึ่งกลางระหว่างจุด (x1, y1) และ (x2, y2)

แสดงว่า x เป็นค่ากึ่งกลางของ x1 และ x2 และ y เป็นค่ากึ่งกลางของ y1 และ y2 จะได้ว่า

จุดที่แบ่งระยะทางเป็นระยะ m:n ดังรูป

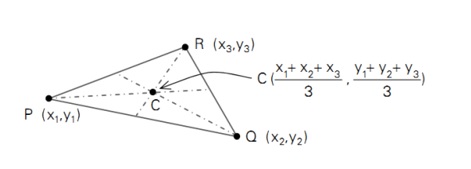
จุดตัดของเส้นมัธยฐานสามเหลี่ยม ดังรูป

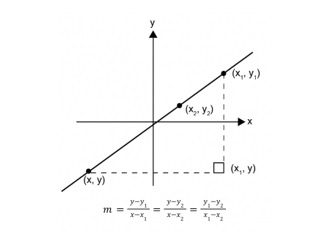
ความชันของเส้นตรง (Slope : m)

คือ อัตราส่วนระหว่างค่า y ที่เปลี่ยนแปลงไป ต่อค่า x ที่เปลี่ยนแปลงไป ใช้ สัญลักษณ์ m โดยค่า m อาจะเป็นบวก หรือลบ หรือเป็นศูนย์ก็ได้

• ถ้า m>0 แสดงว่า เส้นตรงนี้เฉียงขึ้นทางขวา
• ถ้า m<0 แสดงว่า เส้นตรงนี้เฉียงลงทางขวา
• ถ้า m=0 แสดงว่า เป็นเส้นนอนขนานแกน x
• ส่วนเส้นตั้งขนานกับแกน y นั้น m หาค่าไม่ได้ (เป็นอนันต์)

เส้นขนานและเส้นตั้งฉาก

• เส้นตรงที่ไม่ขนานกับแกน y จะขนานกันก็ต่อเมื่อมีความชันเท่ากัน
• เส้นตรงที่ขนานกับแกน y จะขนานกับเส้นตรงที่ขนานกับแกน y เส้นอื่น ๆ ด้วย
• เส้นตรงที่ไม่ขนานกับแกน y จะตั้งฉากกันก็ต่อเมื่อมีความชันคูณกันได้เท่ากับ -1
• เส้นตรงที่ขนานกับแกน y จะตั้งฉากกับเส้นตรงที่ขนานแกน x

ความสัมพันธ์ซึ่งมีกราฟเป็นเส้นตรง

ให้ (x, y) เป็นจุดใด ๆ บนเส้นตรงที่ไม่ขนานกับแกน y และลากผ่านจุด (x₁, y₁) และ (x₂, y₂) จะได้สมการเส้นตรงนี้

ถ้าให้เส้นตรงที่มีความยาว m ตัดแกน y ที่จุด (0, c) จะมีสมการเส้นตรง คือ y = mx+c

ซึ่งจะเรียก c ว่า “ระยะตัดแกน y”

ดังนั้น จุดตัดแกน x คือ ((-c/m), 0)

ซึ่งจะเรียก (-c/m) ว่า ระยะตัดแกน x

ภาคตัดกรวย (conic section หรือ conic)

ในทางคณิตศาสตร์ หมายถึง เส้นโค้งที่ได้จากการตัดพื้นผิวกรวยกลม ด้วยระนาบแบน ภาคตัดกรวยนี้ถูกตั้งเป็นหัวข้อศึกษาตั้งแต่สมัย 200 ปีก่อนคริสต์ศักราชโดย อพอลโลเนียส แห่ง เพอร์กา ผู้ซึ่งศึกษาภาคตัดกรวยและค้นพบสมบัติหลายประการของภาคตัดกรวย

วงกลม

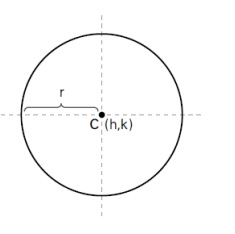
นิยาม : คือ “เซตของคู่อันดับที่อยู่ห่างจากจุดคงที่จุดหนึ่ง เป็นระยะเท่ากัน” เรียกจุดคงที่นั้นว่า จุดศูนย์กลาง (Center; C) และเรียกระยะทางนั้นว่า รัศมี (Radius; r) ดังรูป

สมการวงกลม

• ที่มีจุดศูนย์กลางอยู่ที่จุด (h, k) และมีรัศมียาว r หน่วย จะมีสมการ คือ (x – h)²+ (y – k)² = r²
• สมการรูปทั่วไป x²+y²+Dx+Ey+F=0

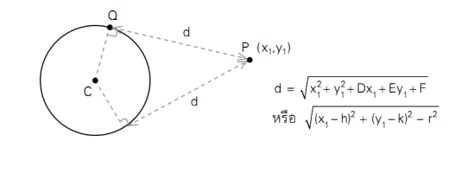
เส้นสัมผัสวงกลม คือ เส้นตรงที่ลากผ่านจุดบนวงกลมเพียงจุดเดียวเท่านั้น โดยเรียกจุด ๆ นี้ว่า จุดสัมผัส มีสมบัติทางเรขาคณิตอย่างหนึ่งของรูปวงกลมที่กล่าวว่า เส้นสัมผัสวงกลมจะตั้งฉากกับรัศมี ณ จุด สัมผัสนั้นเสมอ ดังรูป

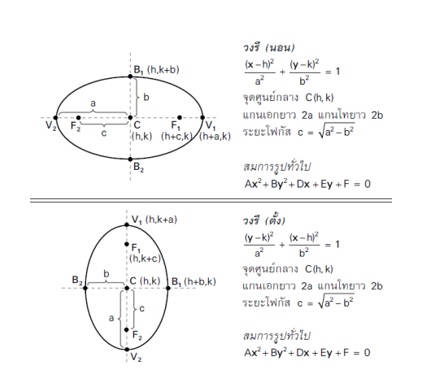
วงรี

นิยาม : ให้ F₁ และ F₂ เป็นจุดใด ๆ จุด P ใด ๆ บนวงรีจะมีผลบวกของระยะจากจุดนั้นไปยังจุด F₁ และ F₂ เป็นค่าคงที่ค่าหนึ่งเสมอ โดยที่ค่าคงที่นี้มีค่ามากกว่าระยะ F₁F₂ หรือก็คือ F₁P + F₂P = k โดยที่ k > F₁F₂ สำหรับทุกจุด P บนวงรี เรียกจุด F₁ และ F₂ ว่า จุดโฟกัส และเรียก k ว่า ผลบวกคงตัว

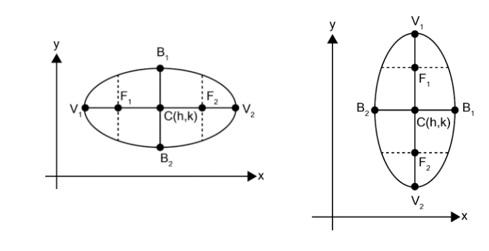
จากรูป เราจะเห็นส่วนประกอบของวงรี ดังนี้

1. จุดศูนย์กลางวงรี (จุด C(h, k)) คือ จุดกึ่งกลางระหว่างจุดโฟกัสทั้งสองจุด กำหนดให้จุดโฟกัสทั้งสองห่างจากจุดศูนย์กลาง c หน่วย จะได้ว่า จุดโฟกัสทั้งสองห่างกัน 2c หน่วย โดย

• ถ้าวงรีเป็นแนวนอน จะได้ว่าจุดโฟกัสคือ (h ± c, k)
• ถ้าวงรีเป็นแนวตั้ง จะได้ว่าจุดโฟกัสคือ (h, k ± c)

2. แกนเอก (จากรูปคือเส้นตรง V1, V2) คือ ส่วนของเส้นตรงที่มีจุดปลายอยู่บนวงรี และลากผ่านจุดโฟกัสทั้งสองจุด กำหนดให้ แกนเอกยาว 2a หน่วย

3.จุดยอดของวงรี(จากรูปคือจุด V₁ และ V₂) คือ จุดปลายของแกนเอก จะเห็นว่า ผลบวกคงตัว จะมีค่าเท่ากับความยาวแกนเอก = 2a หน่วย โดย

• ถ้าวงรีเป็นแนวนอน จะได้ว่าจุดยอดคือ (h ± a, k)
• ถ้าวงรีเป็นแนวตั้ง จะได้ว่าจุดยอดคือ (h, k ± a)
• จุดกึ่งกลางระหว่างจุดยอดทั้งสองจุด คือ จุดศูนย์กลางวงรี

4.แกนโท(เส้นตรง B₁B₂) คือ ส่วนของเส้นตรงที่มีจุดปลายอยู่บนวงรี โดยตั้งฉากกับแกนเอก และผ่านจุดศูนย์กลางวงรี กำหนดให้ แกนโทยาว 2b หน่วย ดังนั้น จุดกึ่งกลางระหว่างจุดปลายของแกนโท คือ จุดศูนย์กลางวงรี

5. เส้นเลตัสเรกตัม (Latus Rectum) คือ เส้นประทั้งสองเส้นในรูปวงรีแนวนอนและวงรีแนวตั้ง ซึ่งเส้น Latus Rectum คือ ส่วนของเส้นตรงที่มีจุดปลาย อยู่บนวงรี (คอร์ดของวงรี) โดยตั้งฉากกับแกนเอกและผ่านจุดโฟกัส

6. ค่าความเยื้องศูนย์กลางของวงรี (e) คือ ค่าที่บอกความรีของวงรี โดย e = c/a โดย

• ค่า e มีค่าอยู่ในช่วง (0, 1)
• หาก e มีค่าเข้าใกล้ 1 วงรีจะรีมาก
• หาก e มีค่าเข้าใกล้ 0 วงรีจะรีน้อย

สมการวงรี

จากรูป

เมื่อพิจารณารูปวงรีทีละด้านแล้วพบว่า จะมีลักษณะโค้งคล้ายรูปถ้วย ซึ่งแต่ละรูปนั้นจะมีจุดโฟกัสอยู่ภายในโค้ง ด้วย และระยะโฟกัส c สามารถหาได้จากค่า a กับ b โดยมีความสัมพันธ์กันในรูปสามเหลี่ยมมุมฉาก ซึ่งมีด้าน a ยาวที่สุด นั่นคือ

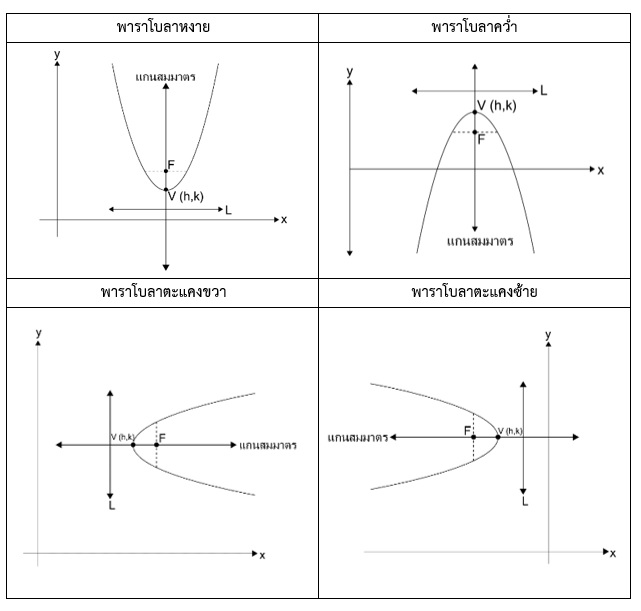
พาราโบลา

นิยาม : ให้ L เป็นเส้นตรงใด ๆ และ F เป็นจุดใด ๆ ที่ไม่อยู่บนเส้นตรง L จุด P ใด ๆ บนพาราโบลาจะมีระยะห่างจากเส้นตรง L เท่ากับ ระยะห่างจากจุด F เรียกจุด F ว่า จุดโฟกัสของพาราโบลา และเรียกเส้นตรง L ว่า เส้น

ไดเรกตริกซ์

จากรูป

เราจะเห็นส่วนประกอบของพาราโบลา ดังนี้

1. จุดยอด (หรือ V(h, k) จากในรูป) คือ จุดที่แบ่งครึ่งส่วนของเส้นตรงที่ลากจากจุดโฟกัสไปตั้งฉากกับเส้นไดเรกตริกซ์ ให้ระยะห่างระหว่างจุดโฟกัสกับจดยอดเท่ากับ a จะได้ระยะห่างระหว่างจุดโฟกัสกับเส้นไดเรกตริกซ์เท่ากับ 2a
2. แกนสมมาตร คือ เส้นตรงที่ตั้งฉากกับเส้นไดเรกตริกซ์ และผ่านจุดโฟกัส และจะผ่านจุดยอดด้วย แกนสมมาตรจะแบ่งกราฟพาราโบลาออกเป็น 2 ส่วนที่สมมาตรกัน
3. เส้นเลตัสเรกตัม (จากรูป คือ เส้นประ) คือ ส่วนของเส้นตรงที่มีจุดปลายอยู่บนพาราโบลา และลากผ่านจุดโฟกัส และขนานกับเส้นไดเรกตริกซ์ เส้นเลตัสเรกตัมยาวเท่ากับ 4a

สมการพาราโบลา

• สมการพาราโบลาหงาย : (x – h)²= 4a(y – k)
• สมการพาราโบลาคว่ำ : (x – h)²= -4a(y – k)
• สมการพาราโบลาตะแคงขวา: (y – k)² = 4a(x – h)
• สมการพาราโบลาตะแคงซ้าย:  (y – k)² = -4a(x – h)

ตัวอย่างข้อสอบเรื่อง เรขาคณิตวิเคราะห์และภาคตัดกรวย

Related Posts

เซต

ตรรกศาสตร์

การให้เหตุผล

จำนวนจริง

ทฤษฎีจำนวนเบื้องต้น

คณิต สรุป เมทริกซ์ คืออะไร พร้อมตัวอย่างข้อสอบ