การให้เหตุผล

สรุปเนื้อหาเรื่อง การให้เหตุผล

การให้เหตุผลคืออะไร

การให้เหตุผลหรือการอ้างเหตุผลทางคณิตศาสตร์ คือ กระบวนการคิดและสื่อความหมายถึงผู้อื่นด้วยภาษา ซึ่งประกอบด้วยข้อความหรือประโยคกลุ่มหนึ่งที่ยกขึ้นมาเพื่อสนับสนุนให้ได้ข้อความหรือประโยคตามมา มักจะแสดงในส่วนของ เหตุ (เรียกข้อความกลุ่มนี้ว่า ข้ออ้าง) และข้อความอีกชุดหนึ่งที่แสดงในส่วนของ ผล (เรียกว่า ข้อสรุป) โดยกระบวนการให้เหตุผล แบ่งออกเป็น 2 วิธี คือ การให้เหตุผลแบบอุปนัย (Inductive Reasoning) และการให้เหตุผลแบบนิรนัย (Deductive Reasoning)

การให้เหตุผลแบบอุปนัย (Inductive Reasoning)

คือ การให้เหตุผลโดยใช้ข้อสังเกตุ ผลการทดลองย่อย หรือความจริงส่วนย่อยที่พบเห็น มาสรุปเป็นข้อตกลง หรือข้อคาดเดาทั่วไป รวมไปถึงคำพยากรณ์ด้วย การหาข้อสรุปหรือความจริงโดยวิธีการให้เหตุผลแบบอุปนัยนั้น ไม่จำเป็นจะต้องถูกต้องทุกครั้ง เนื่องจากเป็นการสรุปผลจากข้อเท็จจริงที่มีอยู่ โดยข้อสรุปที่ได้จะมีความถูกต้องมากเท่าใดนั้นก็จะขึ้นอยู่กับ 3 สิ่ง คือ

• จำนวนข้อมูล ที่มากเพียงพอต่อการสรุปความ
• ข้อมูลหลักฐาน ที่ได้นำมาให้เหตุผลนั้น เป็นตัวแทนที่ดีหรือไม่
• ความซับซ้อนของข้อสรุปที่ต้องการ

ตัวอย่าง

จากการสร้างรูปสามเหลี่ยมในระนาบ พบว่า
เส้นมัธยฐานของสามเหลี่ยมรูป A พบกันที่จุด ๆ หนึ่ง
เส้นมัธยฐานของสามเหลี่ยมรูป B พบกันที่จุด ๆ หนึ่ง
เส้นมัธยฐานของสามเหลี่ยมรูป C พบกันที่จุด ๆ หนึ่ง
ดังนั้น เส้นมัธยฐานของสามเหลี่ยมใดๆ พบกันที่จุด ๆ หนึ่งเสมอ

การให้เหตุผลแบบนิรนัย (Deductive Reasoning)

เป็นการนำความรู้พื้นฐานที่อาจเป็นความเชื่อ ข้อตกลง กฎ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อนและยอมรับว่าเป็นจริง เพื่อหาเหตุผลนำไปสู่ข้อสรุป

ตัวอย่าง

แมงมุมทุกตัวมี 6 ขา และสัตว์ที่มี 6 ขา ทุกตัวมีปีก
ดังนั้น แมงมุมทุกตัวมีปีก

การหาข้อสรุปที่สมเหตุสมผลจากแผนภาพ

การหาข้อสรุปที่สมเหตุสมผลจากแผนภาพนั้น จะใช้กับกรณีของการให้เหตุผลที่เกี่ยวกับตัวบ่งปริมาณ โดยต้องเขียนแผนภาพที่สอดคล้องกับเหตุทุกข้อ (เหตุก็คือ ข้ออ้างหรือสมมดิฐาน) ให้เป็นเผนภาพแบบต่าง ๆ จนครบทุกแบบ ข้อสรุปที่สมเหตุสมผลจะต้องเป็นจริงตามแผนภาพทุกแบบ เพราะข้อสรุปที่สมเหตุสมผลต้องเป็นจริงทุกกรณี ไม่มีกรณีโต้แย้งแม้แต่กรณีเดียว ข้อสรุปใดไม่สอดคล้องกับเผนภาพอย่างน้อย 1 แบบ ก็ถือว่า เป็นข้อสรุปไม่สมเหตุสมผล ดังนั้น เราจึงสามารถแสดงว่าข้อสรุปใดไม่สมเหตุสมผลได้ โดยการเขียนแผนภาพที่สอดคล้องกับเหตุทุกข้อ แต่ขัดแข้งกับข้อสรุปนั้นเพียงแผนภาพเดียวก็พอ

ตัวอย่าง

จงตรวจสอบว่าข้อสรุปที่กำหนดให้ต่อไปนี้สมเหตุสมผลหรือไม่

เหตุ 1. นักกรีทาทุกคนเป็นคนแข็งแรง
2. คนแข็งแรงทุกคนเป็นคนขยัน
3. นที่เป็นคนขขับ
ผล นทีเป็นนักกรีทา

วิธีทำ

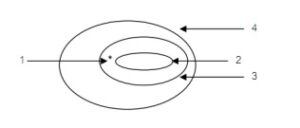
กำหนดให้

สมาชิกหมายเลข 1 คือ นที
กลุ่มสมาชิกหมายเลข 2 ทั้งหมด คือ นักกรีฑา
กลุ่มสมาชิกหมายเลข 3 ทั้งหมด คือ คนแข็งแรง
กลุ่มสมาชิกหมายเลข 4 ทั้งหมด คือ คนขยัน
ในที่นี้จะเห็นได้ว่าข้อสรุปไม่สอดคล้องกับแผนภาพ ดังนั้นข้อสรุปที่ว่า “บที่เป็นนักกรีทา”
จึงเป็นข้อสรุปที่ไม่สมเหตุสมผล

ตัวอย่างข้อสอบเรื่อง การให้เหตุผล

1. 6² – 5² = 1156² – 45² = 1,111556² – 445² = 111,111…5,555,556² – 4,444,445² = xจงใช้การให้เหตุผลแบบอุปนัยเพื่อหาค่า x

2. จงใช้วิธีให้เหตุผลแบบอุปนัยหาจำนวนถัดไปเรียงตามลำดับอีก 3 จำนวนของ 1, 4, 9, 16, …

3. จงพิจารณาผลคูณต่อไปนี้
37 x 3 = 111
37 x 6 = 222
37 x 9 = 333
37 x 12 = 444
จงใช้หลักการอุปนัยในการหาผลคูณที่เท่ากับ 999

4. ถ้าข้อความต่อไปนี้เป็นจริง “คนเลี้ยงปลาทุกคนเป็นชาวสวน” “ชาวสวนบางคนเลี้ยงปลา” และ “นายหวังไม่เป็นชาวสวน” ข้อใดสรุปถูกต้องที่สุด
ก. นายหวังเลี้ยงปลา
ข. นายหวังไม่เลี้ยงปลา
ค. นายหวังเลี้ยงปลาแต่ไม่เป็นชาวสวน
ง. นายหวังไม่เป็นชาวสวน แต่อาจจะเลี้ยงปลา

5. กำหนดเหตุ
1. นกทุกชนิดเป็นสัตว์ที่บินได้
2. สัตว์ที่บินได้ทุกชนิดเป็นสัตว์ที่มี 2 ขา
3. กระรอกบางตัวบิดได้
ข้อสรุปใดต่อไปนี้ไม่สมเหตุสมผล
ก. กระรอกบางตัวมี 2 ขา
ข. กระรอกบางตัวเป็นนก
ค. นกทุกตัวมี 2 ขา
ง. สัตว์ที่บินได้บางตัวเป็นกระรอก

Related Posts

เซต

ตรรกศาสตร์

จำนวนจริง

ทฤษฎีจำนวนเบื้องต้น

คณิต สรุป เมทริกซ์ คืออะไร พร้อมตัวอย่างข้อสอบ

คณิต สรุป ความสัมพันธ์และฟังก์ชัน