สรุปเนื้อหาเรื่อง ความสัมพันธ์และฟังก์ชัน
คู่อันดับ
คู่อันดับประกอบด้วยสมาชิก 2 ตัว เขียนแทนคู่อันดับในรูป (a,b) โดยที่ a เป็นสมาชิกตัวหน้าและ b เป็นสมาชิกตัวหลัง อันดับของสมาชิกถือว่าสำคัญ กล่าวคือการสลับที่กันระหว่างสมาชิกทั้งสองอาจทำให้ความหมายของคู่อันดับเปลี่ยนไปได้
สมบัติของคู่อันดับ
- (a,b) = (b,a) ก็ต่อเมื่อ a = b
- ถ้า (a,b) = (c,d) แล้วจะได้ a = c และ b = d
- ถ้า (a,b) ≠ (c,d) แล้วจะได้ a ≠ c หรือ b ≠ d
หมายเหตุ :
การเท่ากันของคู่อันดับ หมายถึง (x1, y1) = (x2, y2) ก็ต่อเมื่อ
x1 = y1 และ x2 = y2 หรือก็คือ ตัวหน้า = ตัวหน้า, ตัวหลัง = ตัวหลัง
ผลคูณคาร์ทีเชียน
เป็นการกระทำกันระหว่างเซต 2 เซต โดยผลคูณคาร์ทีเชียนระหว่างเซต A และ B เขียนแทนด้วย A×B คือ เซตของคู่อันดับ (a,b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B เขียนอยู่ในรูปแบบ
A×B = {(a,b) | a ∈ A และ b ∈ B}
สมบัติของผลคูณคาร์ทีเชียน
ให้ A, B และ C เป็นเซตใด ๆ และ n(A) คือ จำนวนสมาชิกของเซต A
- A×{} = {}
- {}×A = {}
- A×(B∪C) = (A×B)∪(A×C)
- A×(B∩C) = (A×B)∩(A×C)
- A×(B-C) = (A×B) – (A×C)
- n(A×B) = n(A).n(B)
ความสัมพันธ์จาก A ไป B ให้ A และ B เป็นเซตใด ๆ แล้ว r เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ AB เขียนได้ว่า r = {(a,b) | (a,b) ∈ A×B}
กราฟของความสัมพันธ์
ในระบบแกนมุมฉาก เราสามารถจับคู่หนึ่งต่อหนึ่งระหว่างคู่อันดับของจำนวนจริง (x, y) กับพิกัดของจุดบนระนาบ โดยให้ x เป็นพิกัดแรก และ y เป็นพิกัดหลัง เช่น
ให้ A = {0, 1, 2, 3, 4, 5}
B = {5, 6, 7, …, 20}
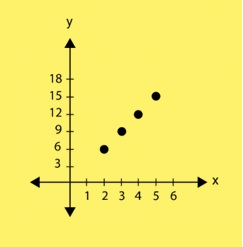
โดย r = {(x, y) ∈ A×B | y = 3x}
แจกแจงสมาชิกได้เป็น r = {(2, 6), (3, 9), (4, 12), (5, 15)}
กราฟที่ได้จะเป็น
สำหรับกรณีที่ r เป็นความสัมพันธ์ของจำนวนจริง มักจะวาดกราฟได้เป็นเส้น ยกตัวอย่างเช่น
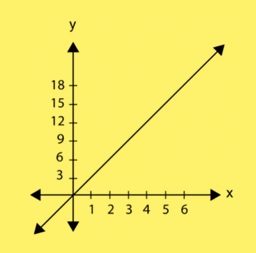
r = {(x, y) ∈ R×R | y = 3x}
กราฟที่ได้ คือ
อินเวอร์สของความสัมพันธ์ คืออะไร
อินเวอร์สของความสัมพันธ์ r คือ ความสัมพันธ์ซึ่งเกิดจากการสลับตำแหน่งของสมาชิกตัวหน้า และสมาชิกตัวหลัง ในแต่ละคู่อันดับที่เป็นสมาชิกของ r เขียนแทนด้วย r-1
โดเมนและเรนจ์ของความสัมพันธ์ คืออะไร
โดเมนของความสัมพันธ์ r คือ เซตของ สมาชิกตัวหน้าของคู่อันดับทุกคู่ ในความสัมพันธ์ r โดเมนของความสัมพันธ์ r เขียนแทนด้วย Dr
Dr = {x | (x, y) ∈ r}
เรนจ์ของความสัมพันธ์ r คือ เซตของ สมาชิกตัวหลังของคู่อันดับทุกคู่ ในความสัมพันธ์ r เรนจ์ของความสัมพันธ์ r เขียนแทนด้วย Rr
Rr = {y | (x, y) ∈ r}
ฟังก์ชัน คืออะไร
คือ ความสัมพันธ์รูปแบบหนึ่งที่สมาชิกในโดเมนแต่ละตัวจับคู่กับ สมาชิกในเรนจ์ของความสัมพันธ์ เพียงตัวเดียวเท่านั้น เช่น
{(1,a), (2,b), (3,c), (4,d)} เป็นฟังก์ชัน
{(1,a), (2,a), (3,a), (4,a)} เป็นฟังก์ชัน
{(1,a), (1,b), (3,c), (4,d)} ไม่เป็นฟังก์ชัน เพราะมี 1 ที่จับคู่กับทั้ง a และ b
การนิยามฟังก์ชัน
ถ้า f เป็นฟังก์ชัน และ (x, y) ∈ f จะได้ว่า y เป็นค่าของฟังก์ชัน f ที่ x เขียนแทนด้วย f(x) หรือ y = f(x) เรียก f(x) = (ค่าในเทอมของ x) ว่า นิยามของฟังก์ชัน
รูปแบบของฟังก์ชัน
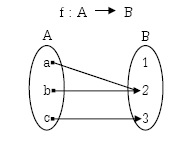 |
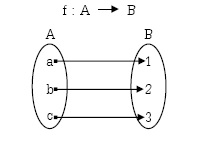
ฟังก์ชันจาก A ไป B f เป็นฟังก์ชันจาก A ไป B เขียนแทนด้วย f:A→B หมายความว่า ทุกสมาชิกใน A ต้องมีคู่กับสมาชิกใน B |
 |
ฟังก์ชันจาก A ไปทั่วถึง B f เป็นฟังก์ชันจาก A ไปทั่วถึง B เขียนแทนด้วย f:A onto→ B หมายความว่า ทุกสมาชิกใน A และ B ต้องมีคู่ |
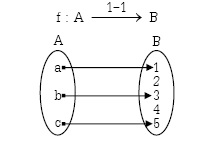 |
ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B เขียนแทนด้วย f:A 1-1→ B หมายความว่า ทุกสมาชิกใน A ต้องมีคู่กับสมาชิกใน B และคู่ไม่ซ้ำ |
วิธีการดูความสัมพันธ์ว่าเป็นฟังก์ชันหรือไม่
- กรณีเป็นกราฟ ให้ลากเส้นตรงให้ขนานกับแกน y หากมีเส้นตรงเส้นใดเส้นหนึ่ง ตัดกราฟเกิน 1 จุด แสดงว่าความสัมพันธ์นั้นไม่เป็นฟังก์ชัน
- เมื่อกำหนดความสัมพันธ์ในรูปสมการ โดยการพิจารณาจากตัวแปร y ถ้าตัวแปร y อยู่ในรูปที่มีเลขชี้กำลังเป็นจำนวนเต็มคู่หรืออยู่ในรูปค่าสัมบูรณ์ ให้พิจารณาไว้ก่อนว่าความสัมพันธ์นั้นไม่ควรเป็นฟังก์ชัน
- รวจสอบโดยใช้หลักการกำหนดดูอันดับ 2 ดูใดๆ ที่ตัวหน้าซ้ำกัน แต่ตัวหลังต่างกัน หากสรุปได้ว่าตัวหลัง
เท่ากัน ดวามสัมพันธ์นี้เป็นฟังก์ชัน ดังนี้ ให้ (a, b) ∈ I และ (a, c) ∈ I ถ้า b = c ก็สรุปได้ว่าเป็นฟังก็ชัน
ฟังก์ชันผกผันหรือฟังก์ชันอินเวอร์ส
ให้ f เป็นฟังก์ชันใด ๆ อินเวอร์สของฟังก์ชัน f เขียนแทนด้วย f-1
ถ้า f-1 เป็นฟังก์ชัน จะเรียก f-1 นี้ว่า ฟังก์ชันอินเวอร์ส ถ้า f-1 เป็นฟังก์ชันของ x จะเขียนได้ว่า f-1 (x) โดยวิธีหา f-1 จะเหมือนกับการหา r-1 (ความสัมพันธ์อินเวอร์ส) โดย
- f-1อาจไม่เป็นฟังก์ชัน
- f-1จะเป็นฟังก์ชัน ก็ต่อเมื่อ f เป็นฟังก์ชันหนึ่งต่อหนึ่ง
- ถ้า f-1 เป็นฟังก์ชันแล้ว f(a) = b จะได้ว่า f-1 (b) = a
ตัวอย่างข้อสอบเรื่อง ความสัมพันธ์และฟังก์ชัน
1. กำหนด f(x) = |x-10| + 4 โดเมนและเรนจ์ของฟังก์ชันนี้คือข้อใด
ก. Df = R, Rf = (-∞, 4]
ข. Df = R, Rf = [4, ∞)
ค. Df = [10, ∞), Rf = (-∞, 4]
ง. Df = [10, ∞), Rf = [4, ∞)
2. กำหนด f(x) = 2×2 + x – 1 จงหาค่าของ f(0) + f(f(f(1)))
ก. 73
ข. 169
ค. 278
ง. 729
3. ข้อใดเป็นฟังก์ชัน
ก. {(0,-1),(0,2),(0,3),(0,5)}
ข. {(-1,0),(0,2),(3,7),(3,9)}
ค. {(1,2),(2,6),(3,-4),(4,0)}
ง. {(2,6),(0,-2),(2,4),(-3,6)}
4.ค่าของ a ที่ทำให้กราฟของฟังก์ชัน y = a(2x) ผ่านจุด (3, 16) คือข้อใดต่อไปนี้
ก. 2
ข. 3
ค. 4
ง. 5
5. กำหนดให้ A = {1, 2} และ B = {a, b} คู่อันดับใดต่อไปนี้เป็นสมาชิกของผลคูณคาร์ทีเชียน A x B
ก. (2, b)
ข. (b, a)
ค. (a, 1)
ง. (1, 2)