คณิต สรุป ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม

สรุปเนื้อหาเรื่อง ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม

ฟังก์ชันเอกซ์โพเนนเชียล คืออะไร

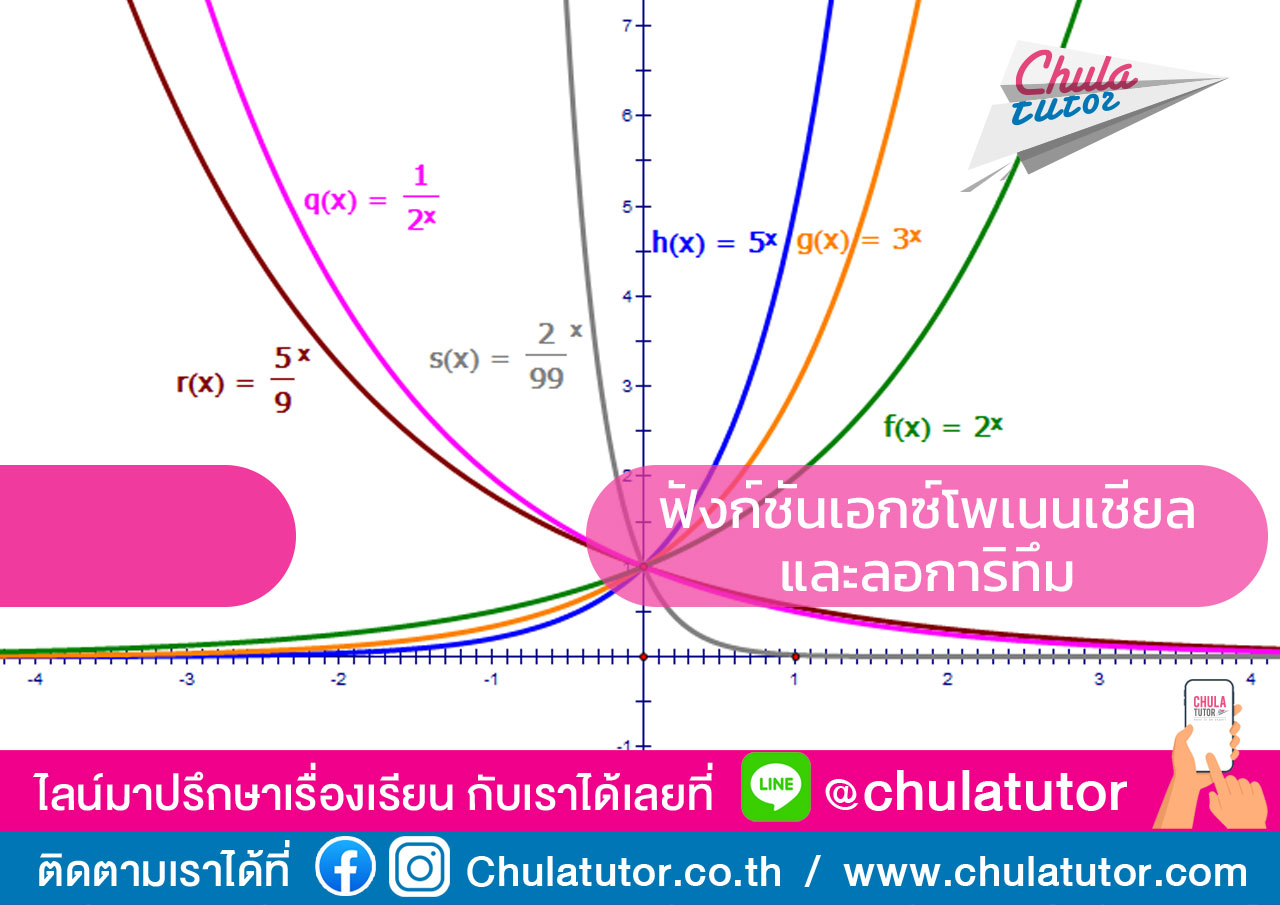
ฟังก์ชันเอกซ์โพเนนเชียล คือ

f = { (x, y) ∈ R × R⁺ / y = a^x , a > 0, a ≠ 1 }

ข้อสังเกต จากข้อกําหนดฟังก์ชันเอกซ์โพเนนเชียล

1. f(x) = 1^x เป็นฟังก์ชันคงตัวเนื่องจาก 1^x = 1 ดังนั้น ในข้อกำหนดฟังก์ชันเอกซ์โพเนนเชียลจึงไม่สนใจฐาน a ที่เป็น 1
2. f(x) = 1^x ไม่เป็นฟังก์ชันเอ็กซ์โพเนนเชียล เนื่องจาก f(x) = 1^x เป็นฟังก์ชันคงตัว
3. จากเงื่อนไขที่ว่า y = a^x , a > 0, a ≠ 1 ทําให้เราทราบได้เลยว่า ฐาน (a) มีอยู่ 2 ลักษณะคือ 0 < a < 1 กับ a > 1
4. ฟังก์ชันเอกซ์โพเนนเชียลจะมีอยู่ 2 ชนิด โดยขึ้นอยู่กับลักษณะของฐาน (a) คือ
   • y=a^x, 0<a<1
   • y=a^x, a>1

 

การแก้สมการเอกซ์โพเนนเชียล

วิธีการ คือ

กําหนดให้ a > 0 , a ≠ 1 และ b > 0 , b ≠ 1

1. . a^∆ = a^◌ ก็ต่อเมื่อ ∆ = ◌ (พยายามทําฐานให้เหมือนกัน)
2. ถ้า a∆ = b^◌ และ a ≠ b แล้ว ∆ = ◌ = 0 เท่านั้น

ข้อควรรู้ : คําตอบที่ได้จากการแก้สมการ ไม่ต้องนํามาตรวจสอบคําตอบ ยกเว้นในกรณีมีการยกกําลังจํานวนคู่ จะต้องตรวจสอบคําตอบด้วย

 

การแก้อสมการเอกซ์โพเนนเชียล

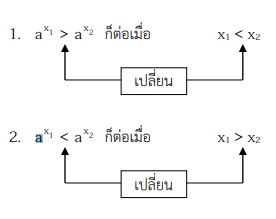
1. ถ้า 0 < a < 1 (ฟังก์ชันลด) แล้ว

สังเกตได้ว่า : สําหรับ 0 < a < 1 เมื่อปลดฐานหรือเติมฐาน เปลี่ยนเครื่องหมายอสมการ

2. ถ้า a > 1 (ฟังก์ชันเพิ่ม) แล้ว

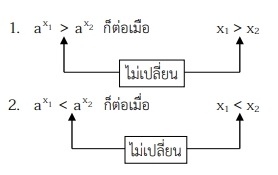
จุดสังเกต : สําหรับ a > 1 เมื่อปลดฐาน หรือเติมฐาน คงเดิมเครื่องหมายอสมการ

 

ฟังก์ชันลอการิทึม คืออะไร

1. ฟังก์ชันอินเวอร์สของฟังก์ชันเอกซ์โพเนนเชียลสามารถเขียนใหม่ได้เป็น { (x, y) ∈ R⁺ ×R / y = log_ax, a > 0, a ≠ 1 }
2. ฟังก์ชันอินเวอร์สของฟังก์ชันเอกซ์โพเนนเชียล ถูกเรียกใหม่ว่า ฟังก์ชันลอการิทึม
3. log_ax อ่านว่า “ลอการิทึมเอกซ์ฐานเอ” หรือ “ล็อกเอกซ์ฐานเอ”

 

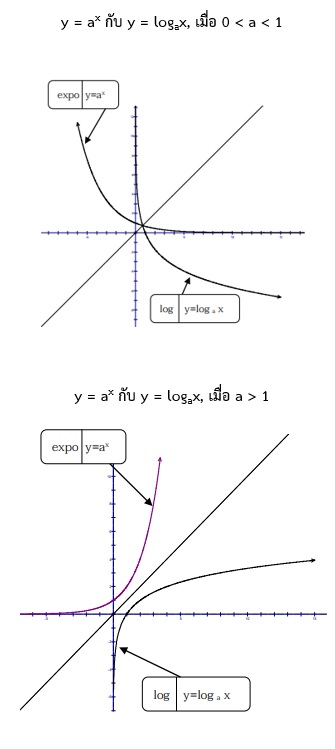
กราฟของฟังก์ชันลอการิทึม

กราฟของฟังก์ชันลอการิทึมทั้ง 2 ชนิด โดยขึ้นอยู่กับลักษณะของฐาน (a) ดังรูป

สมบัติของลอการิทึม

 

การหาค่าลอการิทึม

ลอการิทึมสามัญ หมายถึง ลอการิทึมฐาน 10 ซึ่งนิยมเขียนโดยไม่มีฐานกํากับ เช่น log₁₀7 เขียนแทนด้วย log 7 พิจารณาค่าของลอการิทึมของจํานวนเต็มที่สามารถเขียนในรูป 10ⁿ เมื่อ n ∈ I

log10 = log10¹ = 1

log100 = log10² = 2

log1000 = log10³ = 3

ดังนั้น  log10ⁿ = n

จํานวนจริงบวก N ใด ๆ สามารถเขียนในรูป A ×10ⁿ ได้เสมอ เมื่อ 1 < A < 10 และ n เป็นจำนวนเต็ม

เนื่องจาก

N = A x 10ⁿ

ดังนั้น  log N = log(Ax10ⁿ)

= log A + log10ⁿ

= log A + n

เรียก Log A ว่า แมนทิสซา (mantissa)

เรียก n ที่เป็นจำนวนเต็มว่า คาแรกเทอริสติก (characteristic)

 

แอนติลอการิทึม คืออะไร

1. ถ้า log N = K แล้ว
   N จะถูกเรียกว่า แอนติลอการิทึม (antilogarithm) ของ logK
2. ถ้า log N = K แล้ว
   N จะถูกเขียนสั้น ๆ ได้เป็น antilog (K)
   แสดงว่า N = antilog (K) = 10^k

 

ลอการิทึมธรรมชาติ คืออะไร

ลอการิทึมธรรมชาติ คือ ลอการิทึมที่มีฐานเป็น e โดยที่ e เป็นสัญลักษณ์แทนจํานวนอตรรกยะจํานวนหนึ่งซึ่งมีค่าประมาณ 2.7182818 แสดงว่า log_ex คือ ลอการิทึมธรรมชาตินั่นเอง ซึ่งการเขียนลอการิทึมของ x ฐาน e นิยมเขียน Inx แทน log_ex โดยลอการิทึมธรรมชาติ อาจถูกเรียกว่า “ลอการิทึมแบบเนเปียร์” ก็ได้

 

การแก้สมการลอกาลิทึม

วิธีการ คือ

กําหนดให้ a > 0 , a ≠ 1 และ b > 0 , b ≠ 1

1. log_a∆ = log_a◌ ก็ต่อเมื่อ ∆ = ◌ (พยายามทําฐานให้เหมือนกัน)
2. log_a∆ = ◌ ก็ต่อเมื่อ ∆ = a^◌
3. ถ้า log_a∆ = log_b◌ c และ a ≠ b แล้ว ∆ = ◌ = 1

ข้อควรรู้ : คําตอบที่ได้จากการแก้สมการ จะต้องนํามาตรวจสอบคําตอบว่า ตัวเลขหลัง log จะต้องไม่เป็นจำนวนลบและศูนย์โดยเด็ดขาด อีกทั้งตัวเลขหลัง log ต้องเป็นจำนวนบวกเท่านั้น

 

อสมการลอการิทึม

หลักการ (ดูฐานของ log ถ้าฐาน 0<a<1 เปลี่ยนเครื่องหมายอสมการ, ถ้าฐาน a>1 ไม่เปลี่ยนเครื่องหมายอสมการ)

 

ตัวอย่างข้อสอบเรื่อง ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม