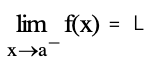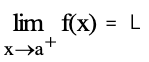สรุปเนื้อหา คณิต ม.ปลาย เรื่อง แคลคูลัส
ลิมิตของฟังก์ชัน
ลิมิตด้านเดียว (One-side limits)
- ลิมิตซ้าย (left-hand limits)
กำหนดฟังก์ชัน f(x) และ a เป็นจำนวนจริง กล่าวว่า ลิมิตของ f(x) เมื่อ x เข้าใกล้ a ทางซ้ายมือก็ต่อเมื่อมีจานวนจริง L ที่ทำให้ค่าของ f(x) เข้าใกล้ L ในขณะที่ x เข้าใกล้ a ทางซ้ายมือ เขียนแทนด้วยสัญลักษณ์
- ลิมิตขวา (right-hand limits)
กำหนดฟังก์ชัน f(x) และ a เป็นจำนวนจริง กล่าวว่า ลิมิตของ f(x) เมื่อ x เข้าใกล้ a ทางขวามือก็ต่อเมื่อมีจำนวนจริง L ที่ทำให้ค่าของ f(x) เข้าใกล้ L ในขณะที่ x เข้าใกล้ a ทางขวามือ เขียนแทนด้วยสัญลักษณ์
ลิมิตสองด้าน (Two-side limits)
เป็นการพิจารณาลิมิตของฟังก์ชันทั้งทางซ้ายและลิมิตทางขวา ของจำนวนจริงจำนวนหนึ่ง นั่นคือ ต้องการพิจารณาค่าของ f(x) ในขณะที่ x เข้าใกล้ a ซึ่งคำว่า “เข้าใกล้ a” หมายถึง เข้าใกล้ทั้งสองด้าน คือ ด้านซ้ายมือของ a และด้านขวามือของ a
การหาลิมิตของฟังก์ชัน
ในการหา เราจะลองแทนค่า x = a ก่อนเป็นอันดับแรก แต่ถ้าบางกรณีที่เราไม่สามารถคำนวณ f(a) ได้ ซึ่งได้กรณีที่การหารด้วยศูนย์ขึ้น ในกรณีนี้ จะมีกรอบของคำตอบของลิมิตดังนี้
การหาลิมิตของฟังก์ชันที่อยู่ในรูปที่ไม่กำหนด
ทฤษฎีบทเกี่ยวกับลิมิต
อนุพันธ์ของฟังก์ชัน
อนุพันธ์ของฟังก์ชัน หมายถึง อัตราส่วนระหว่างผลต่างของตัวแปรตามต่อผลต่างที่น้อยที่สุดของตัวแปรอิสระ หรือผลที่ตัวแปรอิสระเปลี่ยนไปมีค่าเป็นกี่เท่าของตัวแปรอิสระที่เปลี่ยนไปโดยการเปลี่ยนไปของตัวแปรอิสระมีค่าน้อยที่สุด
สรุปสูตรแคลคูลัส
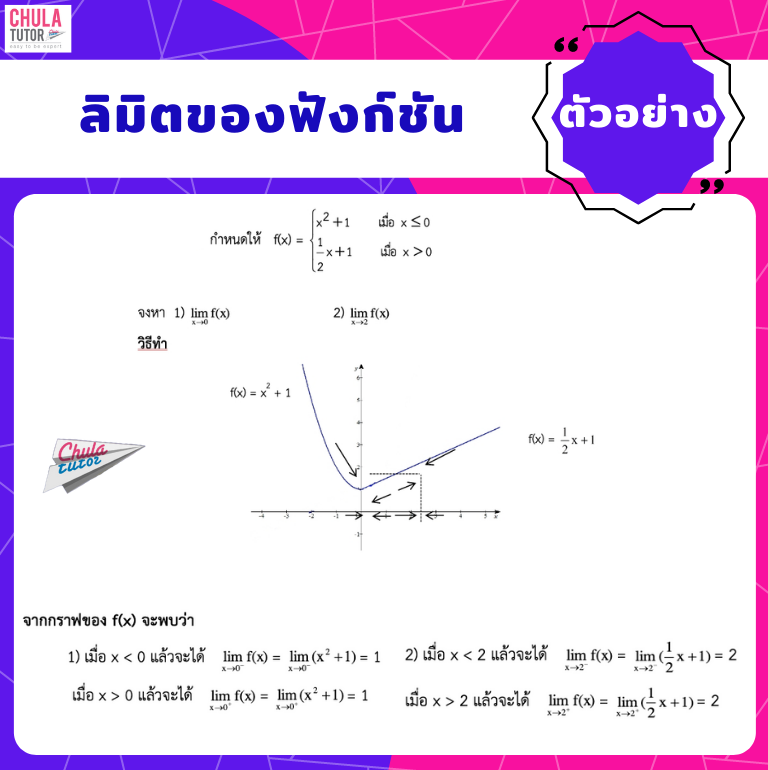
ตัวอย่างข้อสอบเรื่อง แคลคูลัส