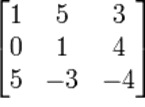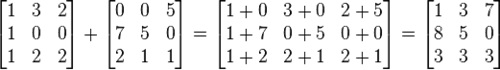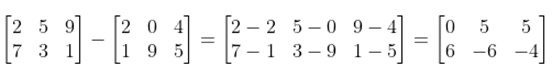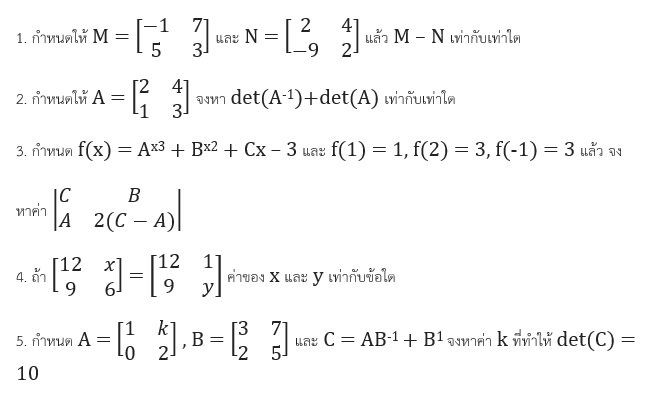สรุปเนื้อหาเรื่อง เมทริกซ์
เมทริกซ์คืออะไร
เมทริกซ์ คือ กลุ่มของจำนวนหรือสมาชิกของริงใดๆ เขียนเรียงกันเป็นรูปสี่เหลี่ยมผืนผ้าหรือจัตุรัส กล่าวคือเรียงเป็นแถวในแนวนอน และเรียงเป็นแถวในแนวตั้ง เรามักเขียนเมทริกซ์เป็นตารางที่ไม่มีเส้นแบ่งและเขียนวงเล็บคร่อมตารางไว้ (ทั้งวงเล็บแบบโค้งและวงเล็บแบบเหลี่ยม) เช่น
โดย
- แถวในแนวนอนของเมทริกซ์ เรียกว่า “แถว”
- แถวในแนวตั้งของเมทริกซ์ เรียกว่า “หลัก”
- จำนวนแต่ละจำนวนในเมทริกซ์ เรียกว่า “สมาชิก” ซึ่งหากเราจะพูดถึงสมาชิกในเมทริกซ์ ก็จะต้องระบุตำแหน่งให้ถูกต้องด้วย เช่น จากรูปด้านล่าง “สมาชิกที่อยู่ในแถวที่ 2 หลักที่ 3 คือเลข 4”
ทั้งนี้ เราจะเรียกเมทริกซ์ที่มี m แถว และ n หลัก ว่า เมทริกซ์ และเรียกจำนวน m และ nว่า “มิติ” หรือ “ขนาด” ของเมทริกซ์
จากรูป
สัญลักษณ์ A = Am x n จะหมายถึง เมทริกซ์ A ซึ่งมี m แถว และ n หลัก โดยที่ ai,j (หรือ aij) หมายถึง สมาชิกที่อยู่ในตำแหน่ง แถว i และ หลัก j ของเมทริกซ์
การบวก ลบ และคูณเมทริกซ์ ทำยังไงได้บ้าง
การบวกเมทริกซ์
เมทริกซ์ที่จะนำมาบวกกันได้นั้น ต้องมีมิติเท่ากัน และการบวกจะนำสมาชิกตำแหน่งเดียวกันมาบวกกันให้ และ เป็นเมทริกซ์ที่มีขนาดเท่ากันสองเมทริกซ์ เราสามารถนิยาม ผลรวม หรือ ผลบวก A + B ว่าเป็นเมทริกซ์ขนาด ที่คำนวณโดยการบวกสมาชิกที่มีตำแหน่งตรงกัน กล่าวคือ หาก
ตัวอย่างเช่น
การลบเมทริกซ์
มิติของเมทริกซ์ที่จะนำมาคำนวณจะต้องเท่ากัน ซึ่งคล้ายกับการบวก แต่ต่างกับการบวกตรงที่สมาชิกข้างในเมทริกซ์จะต้องนำมาลบกัน
การคูณเมทริกซ์
1. คูณด้วยจำนวนจริง
คือ การนำจำนวนจริงค่าหนึ่งคูณกับเมทริกซ์ ซึ่งวิธีการคูณแบบนี้ สามารถนำจำนวนจริงนั้นเข้าไปคูณกับสมาชิกในตำแหน่งในเมทริกซ์ (ต้องคูณทุกตัวแหน่ง) และเมทริกซ์นั้นจะเป็นกี่มิติก็ได้ เช่น
2. คูณด้วยเมทริกซ์
- จำนวนหลักของเมทริกซ์ตัวหน้าต้อง เท่ากับ จำนวนแถวของเมทริกซ์ตัวหลัง
- มิติของเมทริกซ์ผลลัพธ์จะเท่ากับ จำนวนแถวของตัวหน้าคูณจำนวนหลักของตัวหลัง เช่น
ข้อควรรู้เกี่ยวกับการคูณเมทริกซ์
- ไม่มีสมบัติการสลับที่การคูณ นั่นคือ AB ไม่จำเป็นต้องเท่ากับ BA
- เมื่อ AB = BA จะได้
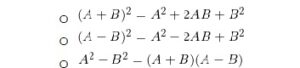
- ถ้า AB = 0 ไม่จำเป็น A ≠ 0 หรือ B ≠0
- ถ้า AB = AC โดยที่ A ≠ 0 ไม่จำเป็น B = C
ตัวอย่างข้อสอบเรื่อง เมทริกซ์